SPC-Control Chart Biểu đồ Xbar-R

Trong bài này chúng ta cùng tìm hiểu về phương pháp tính toán và vẽ biểu đồ Xbar-R

Chọn biểu đồ Xbar-R Chart

1. Copy dữ liệu này và Paste vào Excel (paste Special Unicode text)

Day1 Day2 Day3 Day4 Day5 Day6 #1 167 162 165 162 160 159 #2 165 162 162 163 158 158 #3 159 160 162 162 158 159 #4 162 160 160 164 160 156 #5 161 163 161 168 160 159 Xbar UCL_x X2bar LCL_x R UCL_r Rbar LCL_r

Hoặc tải file về từ link
Xbar-R Chart tài liệu thực hành

2. Công thức tính
      Xem clip để được hướng dẫn dùng hàm trong Excel để tính toán
             

3. Lợi ích của Control Chart Xbar-R

    1. Quan sát sự biến đổi của quá trình (thông qua việc phân tích kết quả đo của sản phẩm tạo ra từ quá trình hoặc thông số của quá trình, tùy theo đối tượng nghiên cứu là gì)

   2. Xbar : hiển thị sự thay đổi của giá trị trung bình của quá trình đang biến đổi ra sao (nếu không có điểm nào vượt ra ngoài giới hạn 3 Sigma UCL và LCL là quá trình đang được kiểm soát)

   3. R Chart : hiển thị sự biến đổi (phân tán) của quá trình, đây cũng được hiểu là sự dao động của quá trình,  (nếu không có điểm nào vượt ra ngoài giới hạn 3 Sigma UCL và LCL là quá trình được cho là chưa có gì bất thường).

Tại sao lại cần cả Xbar và R? vì quan sát giá trị trung bình không phải lúc nào cũng là cho ta cái nhận xét đúng về tình trạng thực tế của quá trình, có thêm R ta quan sát được sự bất thường trong dao động của quá trình để có sự đánh giá đúng hơn.

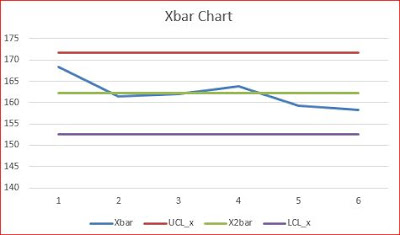
Trong ví dụ trên ta chạy ra được biểu đồ Xbar và R như sau

Ta có thể thấy giá trị trung bình có điểm Day6 là vượt ra ngoài LCL của X các điểm khác cơ bản là nằm trong vùng UCL và LCL, đối với Range tất cả đều nằm trong vùng UCL-LCL.

Ta thay đổi một chút cho nhóm mẫu số 1 như sau

Day1

220

140

159

162

161

Và ta quan sát biểu đồ Xbar và biểu đồ R xem sao

Xbar không thể hiện được sự bất thường của nhóm dữ liệu Day 1, nhưng biểu đồ Range đã cho ta thấy rằng nhóm Day1 có sự dao động RẤT LỚN (vút lên) khỏi đường giới hạn kiểm soát UCL và LCL của Range. Đó chính là lý do mà Chủ nghĩa bình quân không phải lúc nào cũng phản ánh đúng thực tế quá trình.

Chú ý: Việc vẽ biểu đồ bằng Excel này dễ dàng và có thể thêm nhóm dữ liệu mới liên tục, bạn có thể vẽ biểu đồ này với khởi đầu từ 1 đến 2 nhóm dữ liệu. Tuy nhiên theo khuyến cáo thì các bạn không đánh giá quá trình khi số mẫu nhỏ như vậy (nếu nó không có sự dao động quá bất thường như ví dụ trên thì các bạn sẽ Đánh giá quá trình bằng biểu đồ kiểm soát khi bạn có 20 nhóm trở lên).

Mọi trao đổi các bạn hãy comment 

4. Bảng các hằng số trong control chart

Subgroup Size (n)	A2	D3	D4	d2
2	1.880	0	3.267	1.128
3	1.023	0	2.574	1.693
4	0.729	0	2.282	2.059
5	0.577	0	2.114	2.326
6	0.483	0	2.004	2.534
7	0.419	0.076	1.924	2.704
8	0.373	0.136	1.864	2.847
9	0.337	0.184	1.816	2.970
10	0.308	0.223	1.777	3.078
11	0.285	0.256	1.774	3.173
12	0.266	0.284	1.716	3.258
13	0.249	0.308	1.692	3.336
14	0.235	0.329	1.671	3.407
15	0.223	0.348	1.652	3.472
16	0.212	0.364	1.636	3.532
17	0.203	0.379	1.621	3.588
18	0.194	0.392	1.608	3.640
19	0.187	0.404	1.596	3.689
20	0.180	0.414	1.586	3.735
21	0.173	0.425	1.575	3.778
22	0.167	0.434	1.566	3.819
23	0.162	0.443	1.557	3.858
24	0.157	0.452	1.548	3.895
25	0.153	0.459	1.541	3.931

-Viet Nguyen-